Powoli przechodzimy do materiału który dla prawdziwego inżyniera jest czystą przyjemnością. Przy kreśleniu wielościanów można poczuć już potęgę geometrii wykreślnej, a to dopiero wstęp do najtrudniejszej jej części – przenikania figur. Materiał omówiony w tym rozdziale jest już bardzo trudny i wymaga dobrego opanowania transformacji, obrotów, a nawet takich prozaicznych kwestii jak kreślenie elipsy. Nie zaglądajmy do niego póki nie zrozumiemy istoty ww. działów. Na początek trochę definicji i podstawowych zależności.
Wielościanem nazywamy przestrzenną figurę geometryczną utworzoną ze skończonej liczby wielokątów tworzących jego ściany. Bok każdego wielokąta jest wspólny dla dwóch sąsiadujących ze sobą ścian. Wspólne boki tworzą krawędzie wielościanu, a zakończenia krawędzie – jego wierzchołki. Wśród wielościanów możemy wyróżnić dwie kategorie figur: ostrosłupy i graniastosłupy oraz szczególny przypadek wielościan foremny.
Ostrosłupem nazywamy figurę przestrzenną utworzona na wielokącie o n bokach zwanym podstawą ostrosłupa oraz n trójkątów połączonych wspólnym wierzchołkiem zwanym wierzchołkiem ostrosłupa. Odległość między wierzchołkiem a podstawą ostrosłupa nazywana jest wysokością ostrosłupa. Ostrosłupy można dalej dzielić na:
– ostrosłupy proste w których wysokość ostrosłupa tworzy z podstawą kąt prosty, szczególnym przypadkiem jest tutaj ostrosłup prawidłowy w którym dodatkowo podstawa jest wielokątem foremnym (posiada wszystkie boki równe), a krawędzie boczne mają jednakowe długości. najbardziej znane ostrosłupy foremne to czworościan – ostrosłup utworzony przez cztery trójkąty równoboczne oraz ostrosłup prawidłowy czworokątny zwany piramidą.
– ostrosłupy pochyłe, w których wysokość tworzy z podstawą kąt ≠ 90°.
Graniastosłup – figura przestrzenna utworzona z dwóch przystających wielokątów o n bokach równoległych do siebie i zwanych podstawami graniastosłupa, połączonych n równoległobokami zwanych ścianami bocznymi graniastosłupa. Jeżeli ściany boczne sa prostopadłe do podstawy to mamy do czynienia z graniastosłupem prostym, jeśli są nachylone pod kątem ≠ 90°, to mówimy o graniastosłupie skośnym. Możemy też mówić o:
– graniastosłupie prawidłowym – jeśli podstawy sa wielokątem foremnym
– równoległościanie – jeśli podstawy są równoległobokami
– prostopadłościanie – jeśli podstawy sa prostokątami
Wielościan foremny – to wielościan utworzony z przystających do siebie wielokątów foremnych w taki sposób, że wszystkie jego ściany posiadające wspólną krawędź mają te same kąty dwuścienne. Na wszystkich wielokątach foremnych można opisać sferę styczną do jego wszystkich wierzchołków, jak i wpisać sferę styczną do wszystkich ścian, co jest bardzo cenną właściwością przy ich formowaniu. Do wielokątów foremnych należą:
– czworościan- utworzony z czterech trójkątów równobocznych,
– sześcian – utworzony z sześciu kwadratów
– ośmiościan – utworzony z ośmiu trójkątów równobocznych,
– dwunastościan- utworzony z dwunastu pięciokątów równobocznych
– dwudziestościan – utworzony z dwudziestu trójkątów równobocznych
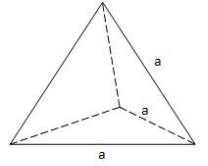

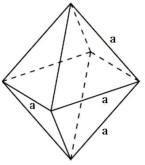
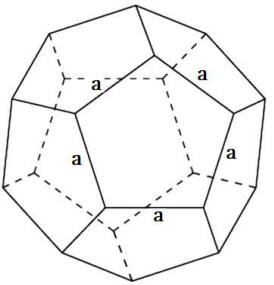

Rys. Wielościany foremne.
Rzuty wielościanów
Do tej pory rysowaliśmy rzuty figur płaskich co znacznie ułatwiało określenie widoczności rzutu. Przy figurach przestrzennych widoczność poszczególnych krawędzi zależy od kierunku patrzenia. Spróbujmy zrzutować na trzy płaszczyzny ostrosłup o podstawie kwadratu. Dla ułatwienia przyjmijmy, że jego podstawa leży na płaszczyźnie π1.

K1, K2, K3 oznaczają kierunki patrzenia, gdzie K1 oznacza kierunek patrzenia w stronę rzutni π1, K2 kierunek patrzenia w stronę rzutni π2, a K3 w stronę rzutni π3 . Jak widać z rzutów odcinki niewidoczne, zasłonięte przez ściany ostrosłupa, to D”S” na rzutni π2 oraz C”’S”’ na rzutni π3. O takich rzutach możemy tez powiedzieć, że – rzut w kierunku rzutni π1, to rzut z góry, rzut w kierunku rzutni π2, to rzut z przodu, rzut w kierunku rzutni π3 , to rzut z boku w tym wypadku z lewej strony.
ZADANIE 1 Wykreśl trzy rzuty czworościanu foremnego którego podstawa leży na rzutni π1.
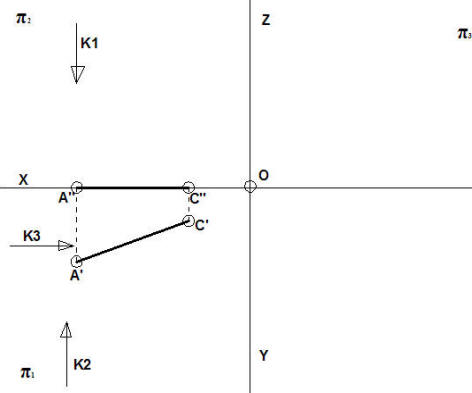
Rozwiązanie: Ponieważ posiadamy tylko jeden bok podstawy konstruujemy pozostałe boki wyznaczając cyrklem łuki o długości A’C’. uzyskujemy punkt B’ który przenosimy na oś X. Teraz kolej na wierzchołek czworokąta. Zgodnie z zasadami geometrii środek czworokąta jest jednocześnie środkiem okręgu opisanego lub wpisanego w trójkąt równoboczny, czyli znajduje sie na dwusiecznych co najmniej dwóch kątów wierzchołkowych.

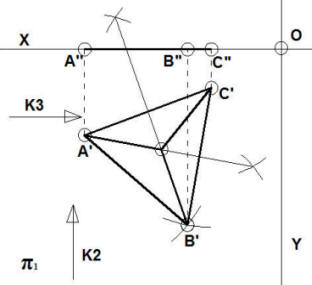
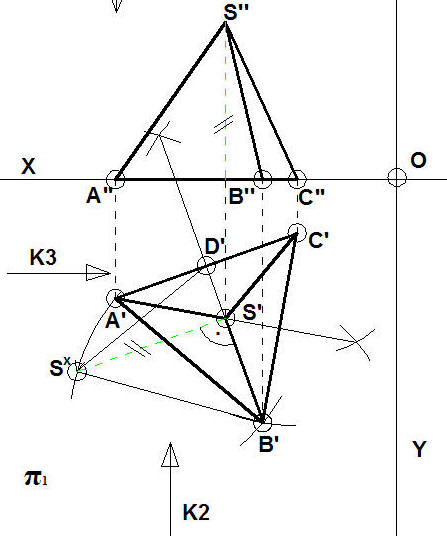
Teraz trudniejsze zadanie, musimy znaleźć wysokość czworokąta, czyli odcinek od podstawy do punktu S” na rzutni π2. Wykonamy w tym celu wykonamy kład trójkąta B’D’S’. Jednym z boków tego trójkąta będzie bok podstawy czworościanu, zakreślamy go np. z p. B’. Następnie z p. S’ prowadzimy prostopadłą do podstawy trójkąta B’D’. Odcinek od punktu przecięcia Sx do p. S’ da nam wysokość czworościanu. Na rys. odcinek oznaczono linią przerywaną w kolorze zielonym. Przenosimy tą wysokość na rzutnię π2 i kreślimy drugi rzut czworościanu.
Teraz wystarczy tylko przenieść punkty na rzutnię π3.
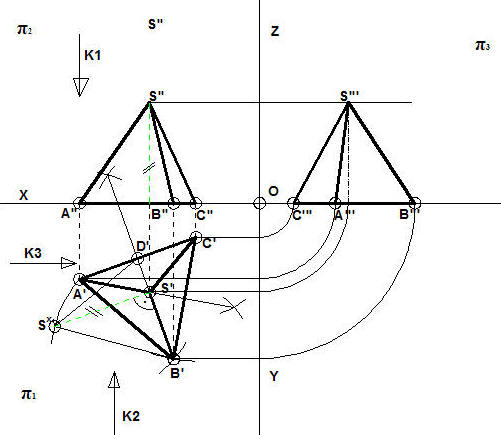
Teraz coś trudniejszego.
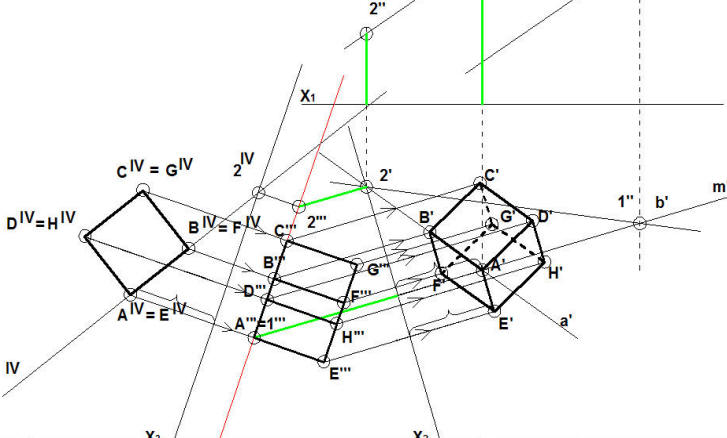
ZADANIE 3. Zbuduj sześcian którego podstawa leży na płaszczyźnie α określonej przez proste a i b, wiedząc, że jeden z jego boków (AB) leży na prostej „a”, a długość boku wynosi 2cm.

Rozwiązanie. Aby narysować sześcian musimy w pierwszej kolejności doprowadzić płaszczyznę w której leży jego podstawa do postaci rzutującej, a następnie obrócić ją o 90°. Uzyskamy w ten sposób kład płaszczyzny α , tym samym będziemy mogli wyznaczyć na niej rzut prostopadły podstawy sześcianu. Mamy dany jeden punkt A będący wierzchołkiem sześcianu. Poprowadźmy przez ten punkt prostą m równoległą do osi rzutów X1 i znajdźmy jej drugi rzut poziomy m’. Przyjmijmy teraz nową oś rzutów X2 ^ m’.

2.Wykonujemy transformację układu odniesienia, w nowym układzie płaszczyzna α jest prostopadła do rzutni i zamienia sie w prostą (kolor czerwony) pokrywającą się jednocześnie z trzecim rzutem prostych a”’ i b”’. Sposób wykonania transformacji pokazuje poniższy rysunek, nowe położenie płaszczyzny α (prostych a i b) znajdujemy odkładając prostopadle do osi X2 odległości pionowe punktów 2 i A od osi X1 (odcinki w kolorze zielonym).
3. Wykonujemy kład płaszczyzny α, w tym celu obieramy nową oś rzutów X3║α , a następnie przenosimy prostopadle do osi odległości dwóch charakterystycznych punktów (w naszym przypadku p.2 i A), uzyskując ich czwarte rzuty AIV i 2IV . Prosta poprowadzona przez te punkty jest kładem prostej a, tym samym kładem płaszczyzny.
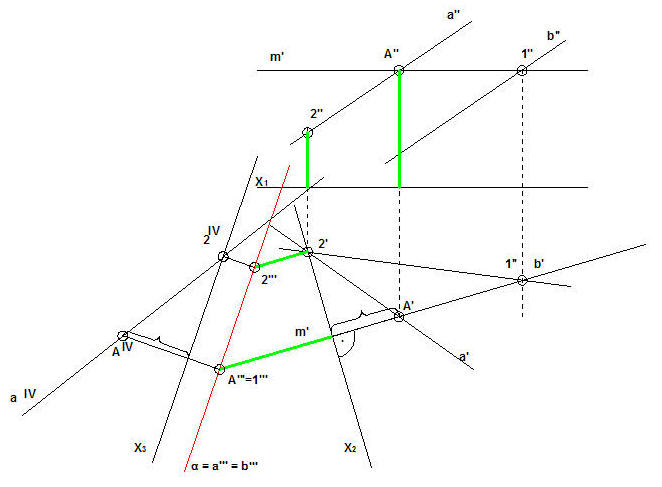
4. Mamy już kład płaszczyzny, możemy więc przystąpić do kreślenia podstawy sześcianu (wielokąt ABCD). Wiemy, że odcinek AB znajduje się na prostej a , więc odkładamy p. B w odległości 2cm od A (tyle wynosi długość boku sześcianu). Następnie prostopadle do prostej a rysujemy kolejne boki uzyskując kwadrat ABCD, ściślej jego czwarty rzut AIVBIVCIVDIV . Wyznaczone w ten sposób punkty pokrywają się z drugą podstawą sześcianu EFGH, przy czym AIV =EIV , BIV =FIV , itd.
5. Przenosimy prostopadle do osi rzutów X3 wszystkie punkty podstawy (ABCD) na rzut prostopadły płaszczyzny α. W nowym położeniu wszystkie punkty znajdą się w jednej linii (punkty A”’B”’C”D”’). Od punktów tych możemy teraz poprowadzić w lewo lub w prawo wysokość sześcianu (odcinek 2cm). Na rysunku poniżej wysokość poprowadzono na lewo od płaszczyzny, uzyskując w ten sposób trzecie rzuty p. E”’F”’G”’H”’.

6. Pozostaje przenieść nasz sześcian na rzutnię poziomą i pionową, na koniec określić widoczność jego krawędzi. Pamiętajmy o prawidłowym przeniesieniu wszystkich odległości. Przykład znajdowania położenia p. E’ pokazuje poniższy rysunek.