Rzutowanie prostych
Dotychczas rzutowaliśmy na dwie, trzy lub cztery płaszczyzny tylko punkt. Spróbujemy teraz zrzutować prostą. Z wiadomości uzyskanych w p. 1 wiemy już, że prostą wyznaczają w przestrzeni co najmniej dwa punkty wzajemnie nie pokrywające się. Aby zrzutować prostą na płaszczyznę, wystarczy zrzutować dwa dowolne jej punkty i przez ich rzuty poprowadzić nową prostą. Inna metoda to wykorzystanie do rzutowania płaszczyzny w której leży prosta, prostopadłej do rzutni. Płaszczyzna taka przecina rzutnię tworząc ślad będący odwzorowaniem prostej. Zobaczmy to na rys.1.

Rys.1 Odwzorowanie prostej „l” na płaszczyznach π1 i π2.
Prosta „l” wyznaczona przez dwa punkty A i B leży w dwóch płaszczyznach prostopadłych do rzutni ε1 ^ π1 i ε2 ^ π2
Rzutami prostej na płaszczyzny są ślady przecięcia się płaszczyzn wyznaczając nowe proste l1 i l2. Posługując się układem płaskim rzutni uzyskujemy znacznie prostszy rysunek (po lewej). W praktyce od teraz rzuty prostych na płaszczyzny prostopadłe będziemy oznaczać małymi literami alfabetu z indeksami zgodnymi z numerem rzutni, np. k1. Nie będziemy tez bez potrzeby zaznaczać punktów na rzutach, rysunek przyjmie wtedy postać na rys.2.


Rys.2 Rzuty prostej na płaszczyzny. Rys 3. Prosta niejednoznaczna w przestrzeni.
Na rys.1 płaszczyzny ε1 i ε2 nie pokrywają się ze sobą, tym samym ich przecięcie wyznacza jednoznacznie położenie prostej „l” w przestrzeni. W praktyce możemy mieć do czynienia z przypadkiem, gdy prosta nie jest prostopadła do żadnej z rzutni, ale leży w płaszczyznach ε1 ^ π1 i ε2 ^ π2 pokrywających się, ε1 = ε2. Rzut takiej prostej jest niejednoznaczny, nie pokazuje jej położenia w przestrzeni. Konieczne jest wtedy wykonanie trzeciego rzutu prostej lub określenie jej w przestrzeni przez zrzutowanie co najmniej jej dwóch punktów.
Szczególne przypadki prostej
Poniżej przedstawiam kilka szczególnych przypadków położenia prostej względem rzutni. Jeden z nich mamy powyżej na rys.2, gdzie prosta jest równoległa do rzutni π1 , stąd na rzucie płaskim jej ślad jest równoległy do osi X1,2. Przypadek prostej równoległej do płaszczyzny π2 pokazuje rys.4. Na kolejnym rysunku mamy przypadek prostej równoległej do obu płaszczyzn, tym samym równoległej na obu rzutach do osi X1,2.


Rys. 6 Prosta „pionowa” L ^ π1 Rys.7 Prosta tzw. „celowa” L ^ π2
Kolejne przypadki szczególne prostych, to proste leżące na rzutni. Jedna z płaszczyzn w których leży prosta pokrywa się wtedy z rzutnią, tym samym jeden z rzutów leży na osi X. Mamy tutaj dodatkowo różne przypadki położenia prostej, w różnych ćwiartkach rzutni.
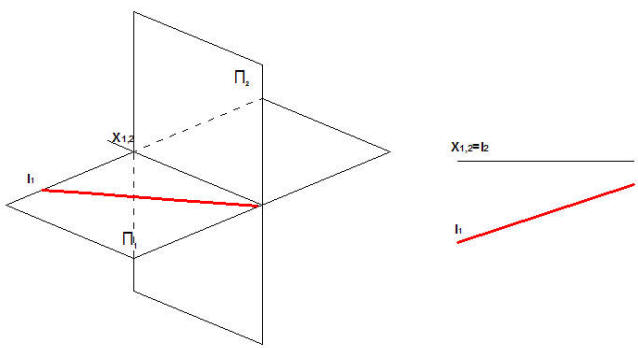
Rys.8 Prosta leżąca w płaszczyźnie rzutni π1 , l = l1
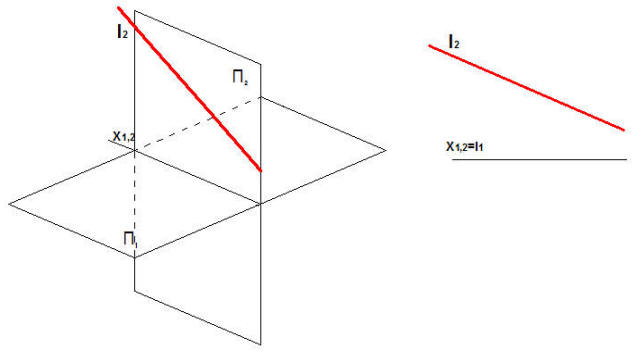
Rys. 9 Prosta leżąca w płaszczyźnie rzutni π2 ,l = l2

Rys.10 Prosta leżąca w płaszczyźnie rzutni π1 , l = l1

Rys. 11 Prosta leżąca w płaszczyźnie rzutni π2 , l = l2
Wzajemne położenie dwóch prostych
Położenie dwóch prostych w przestrzeni może być wzajemnie prostopadłe, wzajemnie równoległe, proste mogą też leżeć w jednej płaszczyźnie lub w różnych płaszczyznach. Proste leżące w jednej płaszczyźnie tworzą płaszczyznę i jeśli nie są równoległe do siebie, to przecinają się w tzw. punkcie właściwym. Punkt ten na rzutach leży zawsze na jednej odnoszącej prostopadłej do osi X. Innymi słowy, jeśli punkt właściwy leży na jednej odnoszącej ^ X, to proste leżą w jednej płaszczyźnie.
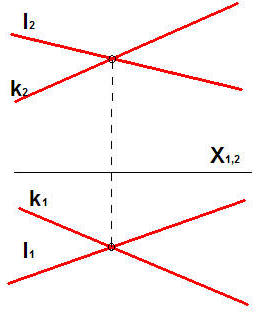
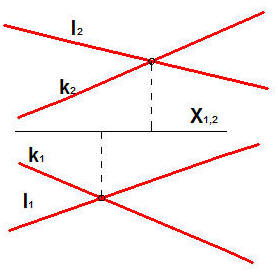
Rys.12 Pary prostych, po lewej przecinających się, leżących w jednej płaszczyźnie, po prawej – para prostych skośnych, leżących w różnych płaszczyznach.

Rys.13 Para prostych równoległych.
Warto przypomnieć, że pary prostych przecinających się i równoległych do siebie wytyczają płaszczyznę. Położenie prostych jest więc automatycznie położeniem płaszczyzny do której te proste należą. Punkt właściwy na rys.12 jest tym samym wspólny dla prostych i dla płaszczyzny. Zapamiętajmy tę właściwość, bo od tej pory zaczyna się tak naprawdę geometria przestrzeni.